Nama : Dewi Anita

TTL : Mojokerto, 06-3-2002

Alamat : Puri- Mojokerto

Read More

BILANGAN BULAT

BILANGAN BULAT

    Bilangan bulat (selanjutnya disingkat menjadi bil. bulat) adalah semua bilangan yang tidak dalam bentuk pecahan atau desimal. Artinya, semua bilangan cacah beserta negatifnya termasuk anggota bil. bulat. Adapun contohnya adalah, -5, -6, -7, -8, 8, 7, 6, 2, dan lainnya. 

JENIS-JENIS BILANGAN BULAT

1. Bilangan bulat positif

Bilangan bulat positif adalah bilangan yang dimulai dari angka satu dan seterusnya. Contohnya adalah 1, 2, 3, 4, 5, 6, 7, …, dan seterusnya. Jika diteruskan, nilainya semakin besar.

2. Bilangan bulat negatif

Bilangan bulat negatif adalah bilangan yang dimulai dari angka negatif satu (-1) dan seterusnya. Contohnya adalah -1, -2, -3, -4, -5, -6, -7, …, dan seterunya. Jika diteruskan, nilainya semakin kecil.

3. Bilangan bulat nol

Bilangan bulat nol adalah bilangan yang hanya terdiri dari angka 0.

Dari ketiga poin di atas, dapat disimpulkan bahwa bil. bulat terdiri dari beberapa jenis bilangan, yaitu bilangan cacah (0, 1, 2, 3, …, dst), bilangan asli (1, 2, 3, 4, …, dst), bilangan prima (2, 3, 5, 7, 11, …, dst), bilangan ganjil (1, 3, 5, 7, 9, …, dst), dan bilangan genap (2, 4, 6, 8, …, dst).

Operasi Hitung 

Secara umum, operasi hitung bilangan ini ada empat, yaitu sebagai berikut.

1. Operasi hitung penjumlahan

Pada penjumlahan, berlaku beberapa sifat berikut.

1.  Sifat asosiatif, yaitu (a + b) + c = a + (b + c)
2. Sifat komutatif, yaitu a + b = b + a
3. Unsur identitas, yaitu a + 0 = 0 + a

Contoh bil. bulat penjumlahan adalah sebagai berikut.

• (2 + 5) + 4 = 2 + (5 + 4) = 11
• 6 + 7 = 7 + 6 = 13
• 8 + 0 = 0 + 8 = 8

2. Operasi hitung pengurangan

Pada pengurangan tidak berlaku sejumlah sifat seperti halnya penjumlahan. Adapun sifat pengurangan adalah sebagai berikut.

a – b = a + (-b)

a – (-b) = a + b

Contoh bil. bulat pengurangan adalah sebagai berikut.

12 – 20 = 12 + (-20) = -8, dengan nilai -8 tersebut adalah bilangan bulat negatif.

1 – (-2) = 1 + 2 = 3

3. Operasi hitung perkalian

Pada perkalian, berlaku sejumlah sifat seperti berikut.

1. Hasil perkalian antara dua bilangan bulat atau lebih harus mengikuti ketentuan berikut.
   • Perkalian antarbilangan bulat positif = positif. Contoh perkaliannya 2 x 3 = 6.
   • Perkalian antarbilangan bulat negatif = positif. Contoh perkaliannya (-2) x (-3) = 6.
   • Perkalian antara bilangan bulat positif dan negatif = negatif. Contoh perkaliannya (-2) x 3 = -6.
2. Sifat asosiatif, yaitu (a x b) x c = a x (b x c)
3. Sifat komutatif, yaitu (a x b) x c = a x (b x c)
4. Sifat distributif, yaitu a x (b +c) = (a x b)  (a x c)

4. Operasi hitung pembagian

1. Hasil pembagian antara dua bilangan bulat atau lebih, harus mengikuti ketentuan berikut.
   • Pembagian antarbilangan bulat positif menghasilkan bilangan positif. Contoh pembagiannya adalah 6 : 3 = 2.
   • Pembagian antarbilangan bulat negatif menghasilkan bilangan positif. Contoh pembagiannya adalah (-6) : (-2) = 3.
   • Pembagian antara bilangan bulat positif dan negatif menghasilkan bilangan negatif. Contoh pembagiannya adalah 6 : (-2) = -3. Perlu diingat bahwa hasil bagi antara dua bil. bulat tidak selalu bil. bulat, contohnya 6 : 4 = 1,5 (angka 1,5 tidak termasuk bilangan bulat).
2. Tidak berlaku sifat komutatif, contohnya 6 : 3 ≠ 3 : 6.
3. Tidak berlaku sifat asosiatif, contohnya (6 : 1) : 3 ≠ 6 : (1 : 3).
4. Jika dibagi dengan nol atau nol sebagai nilai yang dibagi, menghasilkan nilai tak berhingga dan tidak terdefinisi. Contohnya adalah sebagai berikut.
   • 2 : 0 = ~ dan  3 : 0 = ~ , sementara 2 ≠ 3
   • 0 : 2 = 0 dan 0 : 3 = 0, sementara 2 ≠ 3.

Bagaimana Mengurutkan Bilangan Bulat dengan Garis?

Jika Quipperian diberi sejumlah bilangan, lalu kamu diminta untuk mengurutkannya menggunakan garis bilangan, maka hal pertama yang harus kamu lakukan adalah membuat garis bilangan itu sendiri. Adapun contoh garis bilangan adalah sebagai berikut.

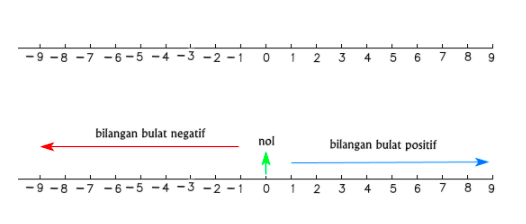
Berdasarkan garis bilangan di atas, yang termasuk bil. bulat negatif, yaitu semua bil. bulat di sebelah kiri nol (ditunjuk panah warna merah). Semakin ke kiri, nilai bilangannya semakin kecil. Sementara itu, yang termasuk bil. bulat positif, yaitu semua bil. bulat di sebelah kanan nol (ditunjuk panah warna biru). Semakin ke kanan, nilai bilangannya semakin besar.

Read More

      Persamaan linier satu variabel adalah suatu kalimat terbuka yang menggunakan tanda sama dengan (=) memuat satu variabel dan berpangkat satu. Bentuk umum Persamaan Linear Satu Variabel adalah ax + b = 0, a ≠ 0, a, b∈R.

    Keterangan: 

x disebut variabel atau peubah 

a disebut koefisien dari x 

b disebut konstanta ax + b terletak di ruas kiri sedangkan 0 terletak pada ruas kanan ruas kiri dan ruas kanan dipisahkan oleh tanda ‘’=’’.

Cara menyelesaikan persamaan linier Untuk menyelesaikan persamaan linier satu variabel ada 4 yaitu dengan cara:  Menambah atau mengurangi kedua ruas dengan bilangan yang sama Contoh dari penyelesaian tersebut adalah:  2x + 5 = x + 8   (menghilangkan angka 5 dengan -5) 2x + 5 – 5 = x + 8 – 5 2x = x + 3   (menghilangkan variabel x dengan -x) 2x – x = x – x + 3 x = 3A

Untuk mengetahui kebenaran hasil jawaban yang kita peroleh, caranya yaitu melakukan subtitusi nilai x = 3 pada soal. Perhatikan langkah berikut! 2x + 5 = x + 8 2(3) + 5 = 3 + 8 6 + 5 = 3 + 8 11 = 11 Karena bilangan pada ruas kiri sama dengan ruas kanan maka dapat dinyatakan hasil yang diperoleh adalah jawaban benar.

Read More